Tangent Handrailing & the Prism Plane

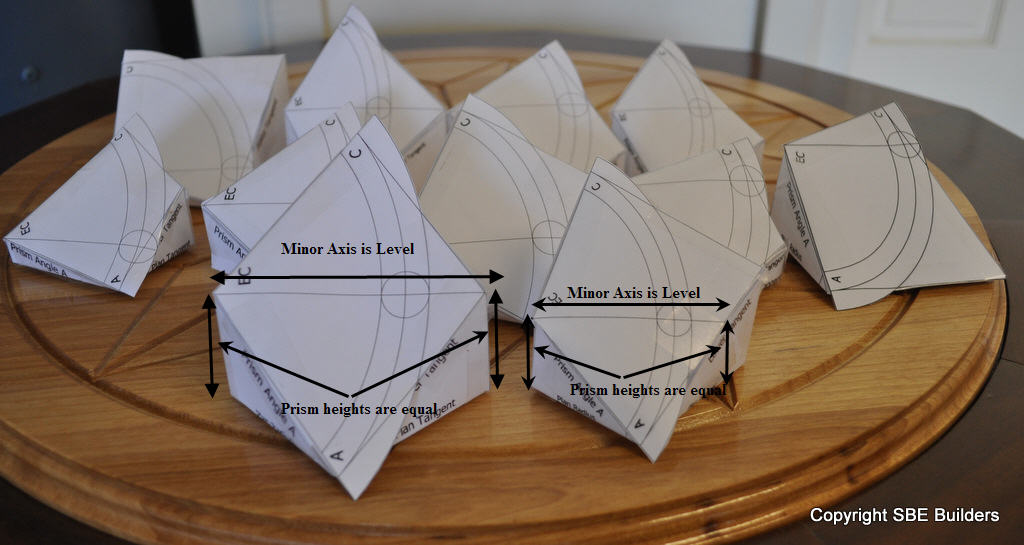
Sometimes it's easy for me to forget what I've already studied. So I decided to put all the Tangent Handrailing studies on one page. Whether,  you're studying the prism plane for the jack rafter claw angle or the prism plane for the for the pitch of plank for the tangent handrailing system, the prism plane is developed using the same geometry.

Tangent HandRailing Trigonometric Development Calculator

or 

Elucidation of the stuff is self evident 

This script returns the Upper & Lower Twist Bevel Angles, Dihedral Angle at Upper Tangent Angle,Angle of the Tangents,Ellipse Semi Major Axis for the tangent handrail geometric drawing. It allows the user to check their geometric drawing of the tangent handrail system. The Rail Block Radius is half the width of the handrailing. It's use to calculate the semi-major axis for the inside and out side of the face mold template. It is used to calculate the Face Mold Width at the Spring Lines. It is used to calculate the Width of Rail Blocks at Twist Bevels. The script also returns the Prism Angles and Prism Heights for any type of prism. Square(quarter circle), obtuse and acute plan angles. The Prism Angles are used to calculate the Face Mold Width at the Spring Lines. The Prism Height at the Spring Lines is calculated from the pitch of plank.

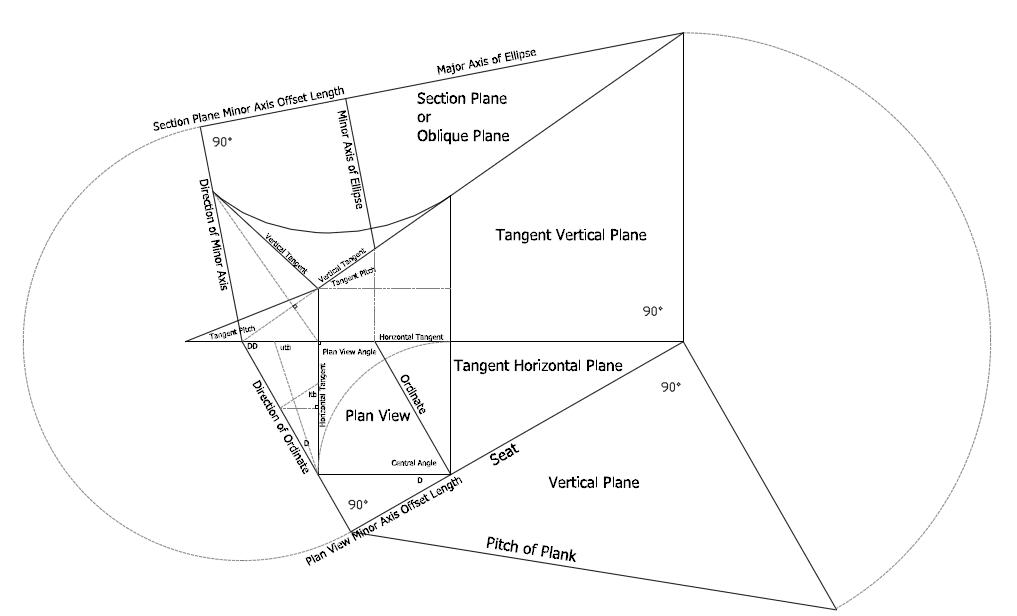
The section plane minor axis offset length can be used to locate the center of the ellipse if your drawing out section planes, like W & A Mowat. The pitch of the plank can be used to check your geometric drawing of the tangent handrail system, if your drawing is based on Robert Riddell's embodying the perfect elucidation of the tangent system.

Pictures of the Study of Tangent Handrailing

Tangent Handrailing Section Planes

Understanding Tangent Handrailing

The file-- Tangent-Handrailing-Section-Planes-Tetrahedrons.pdf contains:

Plates
1: Quarter Circle Plan with Equally Pitched Tangents.
2: Quarter Circle Plan with Short Lower Pitched Tangent.
3: Quarter Circle Plan with the Upper Tangent being Pitched with Level lower Tangent.
4: Quarter Circle Plan with the Upper Tangent  Level with Pitched lower Tangent.
5: Quarter Circle Plan with Short Upper Pitched Tangent.
6: - 15: Yet To do.
16: Quarter Circle Plan with Short Lower Pitched Tangent, correct way to find twist bevel angles.
17: Obtuse Plan with Short Lower Pitched Tangent, correct way to find twist bevel angles.
18: Acute Plan with Short Lower Pitched Tangent, correct way to find twist bevel angles.
19.1: Tangent Handrailing Folding Template. This is the correct way to make a folding template for equal or unequally pitched tangents.
19: Tangent Handrailing Folding Template.  Tetrahedron folding template for equal or unequally pitched tangents.
20: Tangent Handrailing trigonometry code to calculate the plan angles, major axis of the ellipse, upper and lower twist bevel angles and angle of the tangents.
21: Tangent Handrailing tetrahedron relationships to the dihedral angle and twist bevel angles.
22: Rotated Section Planes for Quarter Circle Plan with Equally Pitched Tangents.
23: Rotated Section Planes for Quarter Circle Plan with Unequal Pitched Tangents.
24: Rotated Section Planes for Obtuse Plan with Equally Pitched Tangents.
25: Rotated Section Planes for Obtuse Plan with Unequal Pitched Tangents.
26: Rotated Section Planes for Acute Plan with Equally Pitched Tangents.
27: Rotated Section Planes for Acute Plan with Unequal Pitched Tangents.
28: Step by step instructions for drawing Equally Pitched Tangents.
29: Tangent to Ellipse Geometric Drawing Instructions
30: The Tangent, Bevel and Elliptic Curve
From New Elements of Hand-Railing, by Robert Riddell 1871
31: The Ordinate, its Power and value in the Construction of Wreaths
From New Elements of Hand-Railing, by Robert Riddell 1871

Tangent Handrailing poster board cut out drawings

for 15 different plan tangents 

Tangent handrailing wreath developed from both books. A Treatise on StairBuilding & Handrailing is theoretically geometrical correct, but you need A Simplified Guide to Custom StairBuilding and Tangent Handrailing to understand W & A Mowat. 

Rail Block Laid out for Oblique Cut Method

Oblique Cut Method 

Squaring the Wreath 

JLC Tangent Handrailing - Prismatic Solid Study

Jim Baldwin Traditional Tangent Handrailing Class Study

This drawing shows the ellipse on top of the prism plane. As well as the ellipse developed from plan view ordinates. With the pitch of plank drawn out, it makes it easier to visualize the center point of the ellipse on the prism plane.

Plan View Angle = 108.00000
Plan Central Angle = 72.00000
Plan View Radius = 96.00000

Tangent Angles
Upper Tangent Angle = 32.00000
Lower Tangent Angle = 32.00000
Upper Twist Bevel Angle = 68.94285
Lower Twist Bevel Angle = 68.94285

90° - Upper Twist Bevel Angle = 21.05715
90° - Lower Twist Bevel Angle = 21.05715

Pitch of Plank = 37.68182

Semi Minor Axis = 96.00000
Semi Major Axis = 121.30132

Plan View Angle = 90.00000

Plan Central Angle = 90.00000

Plan View Radius = 96.00000

Tangent Angles

Upper Tangent Angle = 20.00000

Lower Tangent Angle = 32.00000

Upper Twist Bevel Angle = 59.57918

Lower Twist Bevel Angle = 72.84641

Pitch of Plank = 35.87232

Semi Minor Axis = 96.00000

Semi Major Axis = 118.47100