Layover Cuts #2

Purlin Rafters, Roof Sheathing or Dormer Square Tail Fascia Layover Cuts
(Cutting Roof Sheathing with an Edge Bevel)

I was asked to elaborate on roof framing layover cuts. Using the same valley sleeper angle to cut the valley sleeper bevel angle and the layover roof sheathing seems wrong, but it is correct.

Always make some type of test model while you're studying roof framing angles.

Layover cut with an irregular valley. 6:12 & 8:12 roof pitches.

Layover cut with an regular valley. 8:12 roof pitch. 

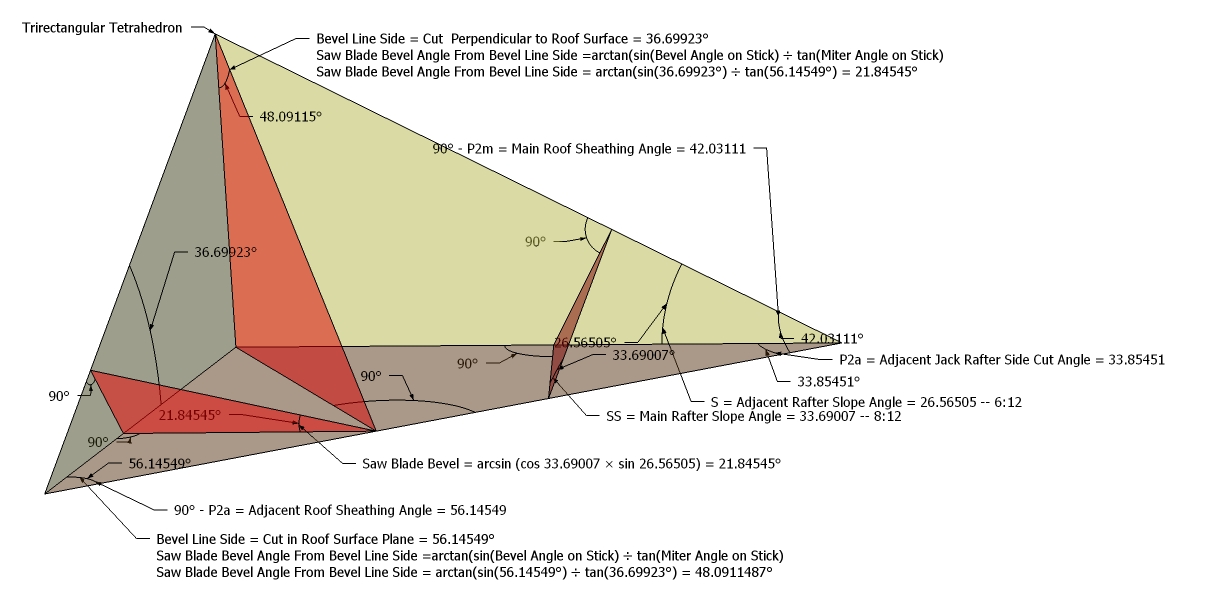
Trirectangular Tetrahedron example for irregular hip roof layover cuts.

C5m Main Hip Rafter Backing Angle = 26.34404
C5a Adjacent Hip Rafter Backing Angle = 15.56481

P2m = Main Jack Rafter Side Cut Angle = 47.96889
90° - P2m = Main Roof Sheathing Angle = 42.03111
P2a = Adjacent Jack Rafter Side Cut Angle = 33.85451
90° - P2a = Adjacent Roof Sheathing Angle = 56.14549

Bevel Angle = arctan(tan(C5m + C5a) × sin(90° - P2a))
Bevel Angle = arctan(tan(26.34404 + 15.56481) × sin(90° - 33.85451°))
Bevel Angle = arctan(tan(41.90885°) × sin(56.14549)) = 36.69923°

Bevel Line Side = Cut Perpendicular to Roof Surface = 36.69923°
Saw Blade Bevel Angle From Bevel Line Side =arctan(sin(Bevel Angle on Stick) ÷ tan(Miter Angle on Stick)
Saw Blade Bevel Angle From Bevel Line Side = arctan(sin(36.69923°) ÷ tan(56.14549°) = 21.84545°

Bevel Line Side = Cut in Roof Surface Plane = 56.14549°
Saw Blade Bevel Angle From Bevel Line Side =arctan(sin(Bevel Angle on Stick) ÷ tan(Miter Angle on Stick)
Saw Blade Bevel Angle From Bevel Line Side = arctan(sin(56.14549°) ÷ tan(36.69923°) = 48.0911487°