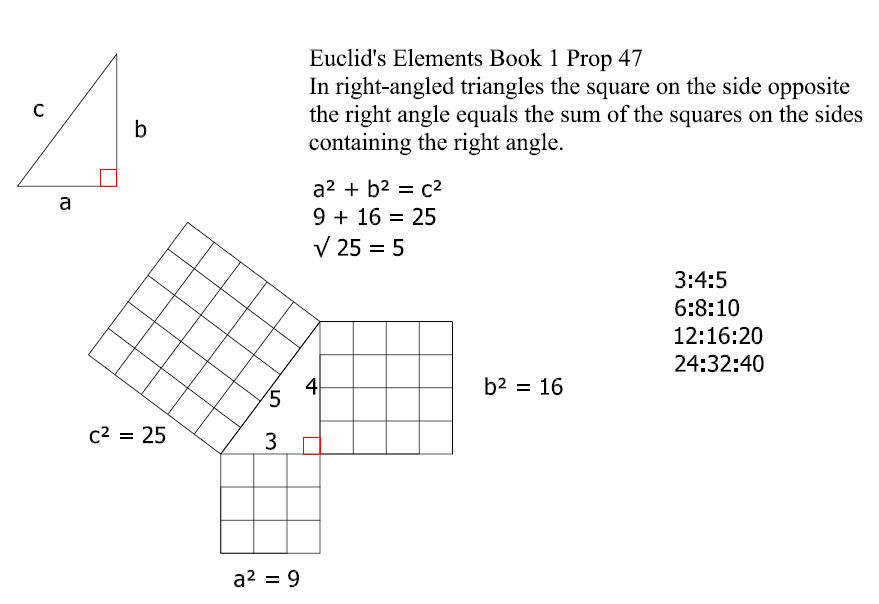
Pythagorean Theorem and Angry Old Men

I haven't used the Pythagorean Theorem  since the 1970's, as a apprentice carpenter to calculate rafter lengths. Roof framing is all about right triangles, but the Pythagorean Theorem is not widely used in calculating the lengths of the roof framing members and calculators use trigonometric ratios to calculate the lengths of the right triangles, not the Pythagorean Theorem . So when I hear or read about the Pythagorean Theorem as the basis of roof framing it brings out the Angry Old Men/Man in me. The Greeks, 1500 years ago, used full scale drawings of the roofs to develop the rafter lengths  and bevels, and used the Pythagorean Theorem to square up the strings they used for the geometric layout of the roof. Full scale geometric layout was used by all carpenters up until the 18th or 19th century and is still used today to scribe the roof framing members. 

Pythagorean Theorem, with sides 3, 4 and 5, a sq x b sq = c sq

Quote from the Stanford Encyclopedia of Philosophy
Stanford Encyclopedia of Philosophy Pythagoras
Proclus does not ascribe a proof of the theorem to Pythagoras but rather goes on to contrast Pythagoras as one of those “knowing the truth of the theorem” with Euclid who not only gave the proof found in Elements I.47 but also a more general proof in VI. 31. 

Speaking of Angry Old Men, it amazing how this article at This is Carpentry brought out the Angry Old Men on Common Rafter Framing.

Common Rafter Framing by Mike Sloggatt @ This is Carpentry

Using trigonometric ratios to calculate the lengths of the right triangles begins with the unit circle.

Trigonometric functions of the angle θ can be constructed geometrically in terms of a unit circle. In this next drawing the unit circle has an radius equal to 1 and the angle θ  equals the roof slope angle of an 8:12 pitched roof.

In this next drawing the unit circle has an radius equal to 1 and the angle θ  equals the hip rafter slope angle of an 8:12 pitched roof.