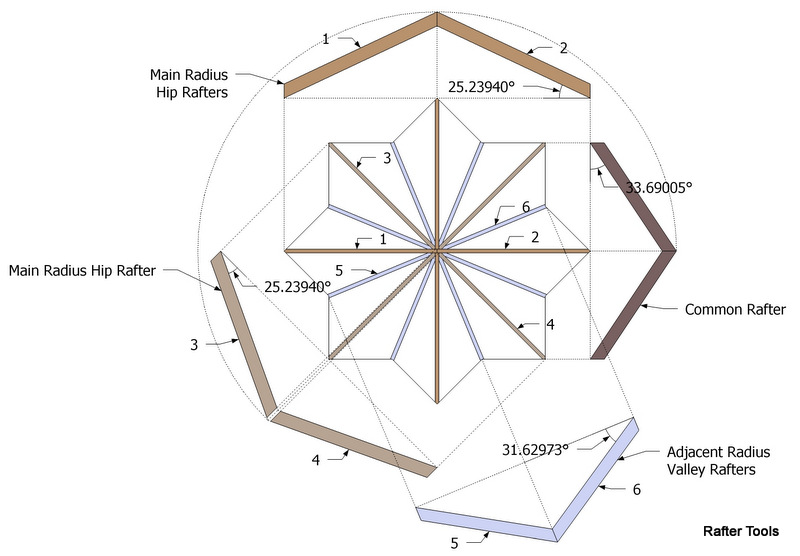
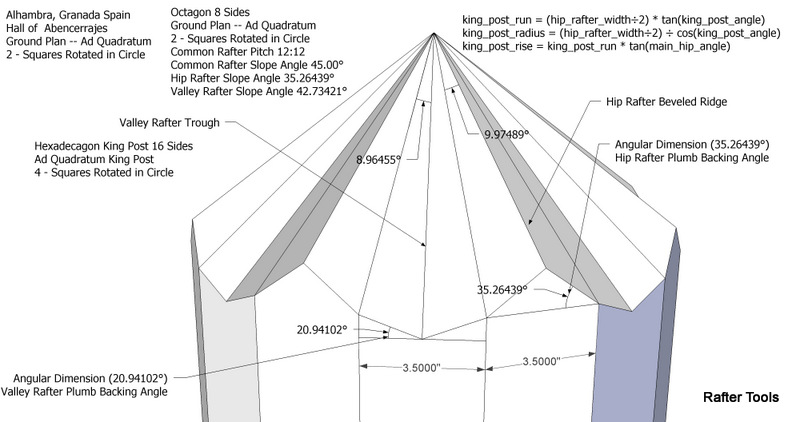
Here's a drawing of the roof. First we need to find the plan angles.
Use the Rafter Tools " Irregular Hip Roof With Equal Overhang" calculator to find the plan angles.
Mark each side of the valley rafter with the "Hip Rafter Backing Depth Mark". Then layout the "Main and Adjacent Hip Rafter Offset Mark Perpendicular To The Hip Run Line". Then make a mark along the hip rafter offset center line the length of the "Hip Rafter Sidecut Mark For Sidecut Angles". Then draw the lines that form the Hip/Valley rafter side cut angles at the foot of the valley rafter. The hip/valley side cut angles are the opposite of the hip/valley rafter side cut angles at the peak of the rafter.
Here's section view of the valley rafter with the valley rafter backing/ bevel cut angles developed from the "Hip Rafter Backing Depth Mark".
Valley Rafter backing/bevel cuts applied to the valley rafter material.
In the Rafter Tools " Irregular Hip Roof With Equal Overhang" calculator click on "View Hip Rafter Angles" to view the hip rafter backing angles, hip rafter side cut angles, jack rafter side cut angles.
Note: Edit: Need to look into the valley rafter side cut angles. Something seems wrong with these angles.
Found it. The correct formula for eave angles greater than 120° with unequal pitches is
(trade secret).... I'll have to update the Rafter Tool calculator with this formula.
Valley rafter side cut angles at the foot of the valley are the same as the side cut angles at the peak of the valley rafter.
Valley backing depth is 5/16" perpendicular to the top of the valley.
Valley rafter plumb backing angles on the end of the square cut valley rafter.
Valley rafter side cut angles at the peak of the valley rafter.
Drawing of valley rafter with plumb cut heights of the two different pitches. The red area could be wrapped in Sheetrock.