Bevel angles for three dimensional connections

Below are a couple of pages from Frank L. Martindale book (1948)
Bevel angles for three dimensional connections
http://steel-link.com/downloads/dl_detail.cfm?recordID=95

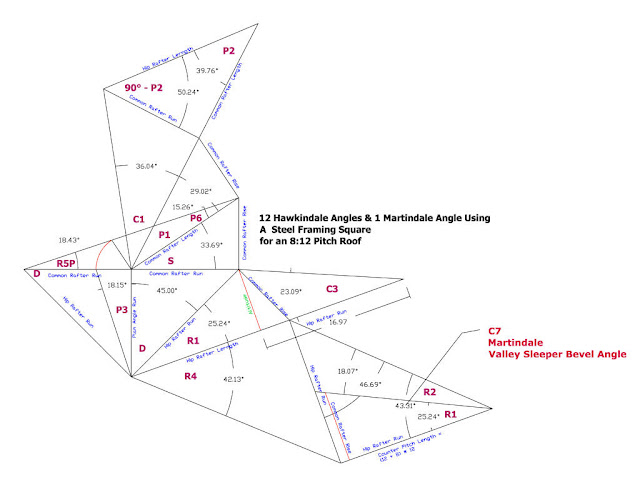
Two of the main bevel angles discussed in the book are, C7 = Inside Valley angle in excess of 90°, is what carpenters refer to as the Valley Sleeper Saw Blade Bevel Angle in roof framing and C8, the sheet metal valley pan flashing.

After discussing my new plan angle formula with Joe Bartok, he remembered seeing something similar in Martindale's Case 4: study of "Location & Formulas for Plan Angles D". Well it turns out that my new plan angle formula was invented 3 years before I was born. So, much for my new and improved plan angle formula.

---

BEVEL ANGLES
FOR THREE DIMENSIONAL CONNECTIONS

TAPERED BIN, HOPPER & TOWER CORNER ANGLES

DIAGRAMS FOR QUICK SOLUTIONS

FORMULAS FOR SPECIAL CONDITIONS

HIP & VALLEY ROOF FRAMING CONNECTIONS

SKETCHES TO LOCATE BEVEL ANGLES REQUIRED

FORMULAS FOR BEVEL ANGLES

ANALYTIC PROOF OF FORMULAS 

TABLES OF HIP & VALLEY BEVEL CONNECTION ANGLES

BY
FRANK  L. MARTINDALE 
REGISTERED PROFESSIONAL ENGINEER

REVISED  BY
ARTHUR 1. MARTINDALE C.E.

REGISTERED PROFESSIONAL ENGINEER ASST. PROFESSOR GENERAL ENGINEERING 
THE  PENNSYLVANIA STATE UNIVERSITY

ANGLE MARKS for BINS & HOPPERS

S & SS = Slope of Sides.
A & A' = Angle in plan view between top edges of bin.
D & D' = Angle in plan view between Valley and top edges of bin.
R1 = Pitch of Valley.
P2 & PP2 = Bevel of valley edge of sloping side of bin.
C5 &  C5' = Angle between Bin side and Valley rafter flange.
C6 &  C6' = Angle between Bin side and a vertical plane thru Valley.
C7 = Inside Valley angle in excess of 90°
C8 = Full inside Valley angle.

NOTE:

Where bin angles are identical with Hip & Valley Roof framing angles, they
have the same marks.
Formulas for angles D & D' for various combinations of slopes and values of A,
are similar to Roof Arrangement angles D, page 19.
The values of D, R1, P2, C5 & C6 are given in Hip & Valley Framing Angle Tables pages 34 to 56 for the given roof slopes. The values for other slopes can be found from formulas page 18.

PREFACE

There is a scarcity of information relating to the solution of three dimensional angles as required for bevel corner angles for tapered bins, hoppers, chutes, towers, spires, masts and other tapered structures, and for hip and valley roof framing angles, and practically no prepared tables for ready reference.

This book is designed to supply such information and to present the subject briefly and concisely and to publish for the first time diagrams and tables of beveled angles that will supply a considerable portion of such angles without computation. Formulas are given for angles not previously included, and new formulas for hip and valley framing angles easier to use.

---

cot(x) represents the cotangent function 1/tan(x).

csc(x) represents the cosecant function 1/sin(x).

sec(x) represents the secant function 1/cos(x).

sin(theta) = a / c
cos(theta) = b / c
tan(theta) = sin(theta) / cos(theta) = a / b

csc(theta) = 1 / sin(theta) = c / a
sec(theta) = 1 / cos(theta) = c / b
cot(theta) = 1/ tan(theta) = b / a

---

tan D = bb ÷ (aa * sec E  - bb * tan E)
tan D = 8.6514 ÷ ( (12 * sec(16))  - (8.6514 * tan(16))) = 40.85633°

tan D' = bb ÷ (aa * sec E  - bb * tan E)
tan D' = 8.6514 ÷ ( (12 * sec(16))  + (8.6514 * tan(16))) = 30.03368°


90° - arctan DD = ((bb * sec E)  - aa * tan E)) ÷ aa
90° - arctan DD = ((8.6514 * sec(16))  - (12 * tan(16))) ÷ aa = 65.14385°



90° - arctan DD = ((bb * sec E)  + aa * tan E)) ÷ aa
90° - arctan DD = ((8.6514 * sec(16))  + (12 * tan(16))) ÷ aa = 43.96643°