Formulas arise from the geometry

Joe Bartok said Formulas arise from the geometry. This is the cornerstone of all my new/old trigonometry formulas after I meet Joe. Before I meet Joe I would draw 20 different triangles on the same piece of paper to calculate the roof angles. Now my preferred method is to first draw out a tetrahedron. If I can't find the angles I'm looking for in the tetrahedron, I'll take a tetrahedron slice cut from the rafter. Then I'll unfold the tetrahedron slice and finally I'll develop the correct tetrahedron showing the relationships of the different roof framing angles that I can use to develop the trigonometric formula.

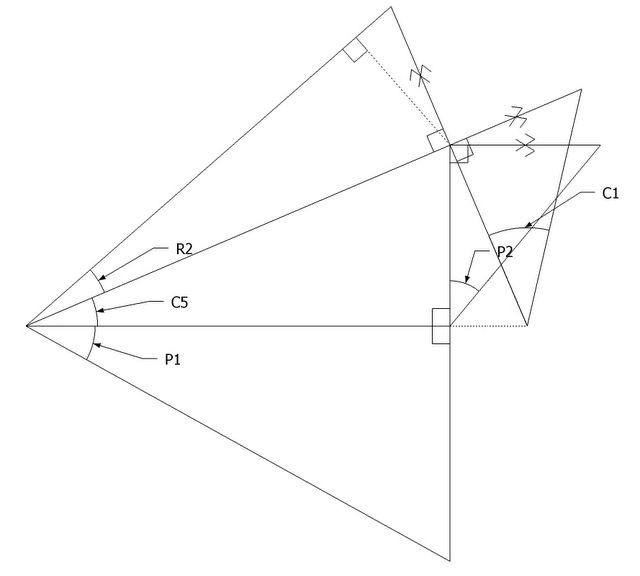
Tetrahedron Slice

Miter Angle R2 -- Witches Cut -- Square Tail Fascia Miter Angle on the Side Of Hip Rafter

Saw Blade Bevel C1
Develops Bevel Angle 90 - R3 on the top edge of the hip rafter material.

Use C1 for the saw blade bevel angle along the miter line (R2) on the side of the hip rafter.

C1 = Saw Blade Bevel Angle = arcsin( cos ( Pitch Angle ) * cos( Plan Angle ))

or

Known Angles

1. R2
2. R3
3. C1
4. C2

C1 = Saw Blade Bevel Angle = arctan( cos ( R2 ) * tan( R3 ))

C1 = Saw Blade Bevel Angle = arcsin( sin ( R3 ) * cos( C2 ))

C1 = Saw Blade Bevel Angle = arccos( sin ( C2 ) ÷ sin( R2 ))

C1 = Angle B in the tetrahedron

Tetrahedron Trigonometric Identity Formulas

by Joe Bartok

Angle B = arccos( sin ( D ) ÷ cos ( E ))

Angle B = arccos( cos ( A ) ÷ cos ( C ))

Angle B = arcsin ( sin ( A ) × cos ( D ))

Angle B = arcsin ( tan ( E ) × tan ( C ))

Angle B = arctan( tan ( A ) × sin ( E ))

Angle B = arctan( sin ( C ) ÷ tan ( D ))

1. C1 = arccos( sin ( C5 ) ÷ cos ( 90 - P1 ))
2. C1 = arccos( cos ( P2 ) ÷ cos ( R2 ))
3. C1 = arcsin ( sin ( P2 ) × cos ( C5 ))
4. C1 = arcsin ( tan ( 90 - P1 ) × tan ( R2 ))
5. C1 = arctan( tan ( P2 ) × sin ( 90 - P1 ))
6. C1 = arctan( sin ( R2 ) ÷ tan ( C5 ))