I asked Joe Bartok to help me with the saw blade bevel angle on the Tréteaux Dit Cadet task model. I had some inconsistencies in my SketchUp drawings and it resulted in inconsistencies in the results of Joe's formulas. So I made drew up some new control files and sure enough Joe's formulas for the saw blade bevel angle at the foot of the trestle-sawhorse-hip rafter rotated into the roof surface plane for the Parallelogram Prism were correct.

tréteau à devers

Research notes:
-----------------------------------------------------------------------------

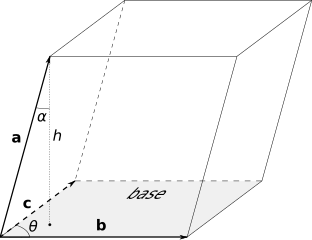
Parallelepiped

In three dimensional geometry a parallelepiped is a prism whose faces are all parallelograms.

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms.

http://en.wikipedia.org/wiki/Parallelepiped

Trihedral Angle

-----------------------------------------------------------------------------------------------------

First I drew out an equal pitched 8:12 roof.

Angular Dimension (27.13381°)
Hip Rafter Rotated Slope Angle = arctan( tan ( Hip Rafter Backing Angle) ÷ tan (Jack Rafter Side Cut Angle ))
Hip Rafter Rotated Slope Angle = arctan( tan ( 23.09347) ÷ tan (39.76216 )) = 27.13381°
Prism Miter Angle = 50.23784°
Prism Saw Blade Bevel Angle = arctan(sin 50.23784° ÷ tan 27.13381°) = 56.30993°
Profile Rafter Slope Angle = 33.69007°
90.00° - 33.69007° = 56.30993°

Angle on Sloped Face of Prism = arccos(cos 50.23784° * cos 27.13381°) = 55.30485°

Then I re-drew the Tréteaux Dit Cadet task model, but without all of the actual sawhorse lines.

Angular Dimension (75.51397°)

Hip Rafter Rotated Slope Angle = arctan( tan ( Hip Rafter Backing Angle) ÷ tan (Jack Rafter Side Cut Angle ))

Hip Rafter Rotated Slope Angle = arctan( tan ( 45.26145°) ÷ tan (14.61316°)) = 75.51399°

Prism Miter Angle = 14.61316°

Prism Saw Blade Bevel Angle = arctan(sin 75.38684° ÷ tan 75.51399°) = 14.03622°

90.00° - 14.03622° = 75.96378°

Angle on Sloped Face of Prism = arccos(cos 75.38684° * cos 75.51399°) = 86.38170°

After I developed the formula to calculate the Hip Rafter Rotated Slope Angle everything fell into place.

Hip Rafter Rotated Slope Angle = arctan( tan ( Hip Rafter Backing Angle) ÷ tan (Jack Rafter Side Cut Angle ))

Joe Bartok's formula for Compound Angle Formulas

tan Saw Blade Bevel = sin Angle of Saw Travel ÷ tan Angle on the Adjoining Face

Angle of Saw Travel = 75.38684° = Roof Sheathing Angle

Angle on the Adjoining Face = 75.51399° = Hip Rafter Rotated Slope Angle

Prism Saw Blade Bevel Angle = arctan(sin 75.38684° ÷ tan 75.51399°) = 14.03622°

Profile Rafter Slope Angle = 75.96376°

90.00° - 14.03622° = 75.96378°

It turns out that the Prism Saw Blade Bevel Angle = 90° - Profile Rafter Slope Angle.

The next angle we need to check is the Hip Rafter Tilt from Plumb, Angular Dimension (19.17417°).

Math Notes:

Profile Slope Angles

SS = side of hip rafter rotated into roof surface

S = DP side of hip rafter …. DP = Devers De Pas -à tilt/ skewed from ground plane

SS = 75.96376 -- plan angle DD = 42.92997° -- backing angle C5m = 45.26145°

S = 74.95720 -- plan angle D = 47.07003° -- backing angle C5a = 41.12961°
Hip Slope Angle R1 = 69.84428°

P2m = arctan (cos SS ÷ tan DD)
P2m = arctan (cos 75.96376° ÷ tan 42.92997°) = 14.61316°
90 - P2m = arctan (cos 75.96376° ÷ tan 42.92997°) = 75.386839°

H1 = Tilted Hip Rafter Slope Angle = arctan( tan ( Hip Rafter Backing Angle) ÷ tan (Jack Rafter Side Cut Angle ))
H1 = arctan( tan ( C5m ) ÷ tan ( P2m ))

H1 = arctan( tan ( 45.26145° ) ÷ tan ( 14.61316° )) = 75.51399°

ΣR4B = Angle on Sloped Face of Prism = arccos( cos P2m × cos H1 )

ΣR4B = Angle on Sloped Face of Prism = arccos( cos 75.38684° × cos 75.51399° ) = 86.38170°

H2 = Horizontal Plane Rotation for Tilted Hip Rafter -- DD-dp

H2 = D - ( 90° - ΣR4B )

H2 = 47.07003° - ( 90° - 86.38170° ) = 43.45173°
or

H2 = arctan( sin R1 × tan C5m )
H2 = arctan( sin 69.84428° × tan 45.26145°) = 43.45178°

HDP = Horizontal Plane Rotation for Tilted Hip Rafter for Footprint From Eave Line
HDP = D - H2
HDP = 47.07003° - 43.45173° = 3.6183°

H3 = Vertical Plane Rotation for Tilted Hip Rafter

H3 = arctan( cos R1 × tan H2 ) ÷ sin R1

H3 = arctan( cos 69.84428° × tan 43.45173° ) ÷ sin 69.84428° = 19.17416°

H4 = Prism Saw Blade Bevel Angle Along side of Hip Rafter Rotated into the Roof Surface Plane

H4 = arctan( sin 90° – P2m ÷ tan H1 )

H4 = arctan( sin 75.38684° ÷ tan 75.51399° ) = 14.03622°

Joe's Sketch of an isometric projection of the Adjusted Dihedral Angle.

-----------------------------------------------------------------------

H5 = Hip Rafter Miter Angle on Side Of Hip Rafter at Peak
H5 = arctan(( sin 90-P2m ÷ tan C8) ÷ cos 90-P2m)

Results for an equal pitched roof
8:12 , 90° Eave Angle
C8 = 23.09341 + 23.09341 = 46.18682

arctan(( sin 50.23784 ÷ tan 46.18694) ÷ cos 50.23784)=49.06626°
arctan(cos 50.23784 ÷ ( sin 50.23784 ÷ tan 46.18694)) = 40.93374
arctan(( sin 90-P2m ÷ tan C8) ÷ cos 90-P2m)=49.06626°

SS = 75.96376 -- plan angle DD = 42.92997° -- backing angle C5m = 45.26145°
S = 74.95720 -- plan angle D = 47.07003° -- backing angle C5a = 41.12961°
Hip Slope Angle R1 = 69.84428°

C8 = C5m + C5a = 45.26145° + 41.12961° = 86.39085°
P2m = arctan (cos SS ÷ tan DD)
P2m = arctan (cos 75.96376° ÷ tan 42.92997°) = 14.61316°
90 - P2m = arctan (cos 75.96376° ÷ tan 42.92997°) = 75.386839°

H5 = Hip Rafter Miter Angle on Side Of Hip Rafter at Peak
H5 = arctan(( sin 90-P2m ÷ tan C8) ÷ cos 90-P2m)
H5 = arctan(( sin 75.386839° ÷ tan 86.39097°) ÷ cos 75.386839°) = 13.59932°

tan Saw Blade Bevel = sin Angle of Saw Travel ÷ tan Angle on the Adjoining Face
H6 = Saw Blade Bevel Angle along Miter Line H5
H6 = arctan(sin 13.59932° ÷ tan 75.38684°) = 3.508105°

Checking the traditional layout geometry against the trigonometry formulas. The traditional layout geometry is correct. This is one of the main reasons to study the trigonometric formulas. It's easy to draw out the traditional layout geometry incorrectly for rafters. Using trigonometry we can check the traditional layout geometric techniques in books, like Louis Mazerolle's book, Traite Theorique Et Pratique De Charpente, planche 27-28 and know we understand the traditional layout geometry technique and we're drawing it out correctly. There's nothing worst then to draw out and cut the rafters only to find out that the traditional layout geometry was never correct, or you didn't interpret the traditional layout geometry in the books correctly.

Purlin Rafters at Hip Rafter Rotated Into Roof Surface

H7 = Miter Angle on Side Face Parallel To Roof Surface = 90° + P2m = 104.61316
H8 = Bevel Angle On Top Edge Face Perpendicular to Roof Surface = 90.00°
H9 = Saw Blade Bevel Angle Along Miter Angle on Side Face = 0.00°

Jack Rafters at Hip Rafter Rotated Into Roof Surface

H10 = Miter Angle on Side Face = 90°
H11 = Bevel Angle On Top Edge Set in Roof Surface = P2m
H12 = Saw Blade Bevel Angle Along Miter Angle on Side Face = P2m

For the jack purlin rafter on the DP side.

H13 = Jack Purlin Miter Angle on Face Perpendicular to Roof Surface, Lower Claw

H13 = arctan( sin ( P2 ) ÷ tan ( Valley Sleeper Saw Blade Bevel Angle ))

H13 = arctan( sin ( 76.42666 ) ÷ tan ( 3.60903))= 86.2876°

H14 = Jack Purlin Miter Angle on set in Roof Surface

H14 = 90 - P2

H15 = Purlin Lip/Claw Angle on DP Side, Upper Claw

H15 = arctan( cos ( P2 ) ÷ tan (90 – Valley Sleeper Saw Blade Bevel Angle ))

H15 = arctan( cos ( 13.57334 ) ÷ tan ( 90-3.60903))= 3.50849°

Angular Dimension (3.50849°)

SS = 75.96376

S = 74.9572

P2a = 13.57334

Valley Sleeper Saw Blade Bevel Angle = arctan(tan(90-S) *sin(P2))

Valley Sleeper Saw Blade Bevel Angle = arctan(tan(90-74.9572) *sin(13.57334)) =3.60903

Jack Purlin Claw Angle = arctan( cos ( P2 ) ÷ tan (90 – Valley Sleeper Saw Blade Bevel Angle ))

Jack Purlin Claw Angle = arctan( cos ( 13.57334 ) ÷ tan ( 90-3.60903))= 3.50849

For an equal pitched 8:12 roof.

For the jack rafter on the DP side.

H16 = Jack Rafter Miter Angle on Face Perpendicular to Roof Surface, Upper Claw Angle

H16 = Upper Jack Rafter Claw Angle = arctan( sin ( P2 ) × tan (Valley Sleeper Saw Blade Bevel Angle ) )

H16 = Upper Jack Rafter Claw Angle = arctan(sin 39.76216 × tan (43.81306)) = 31.53479°

H17 = Jack Rafter Miter Angle on set in Roof Surface
H17 = 90 - P2

H18 = Jack Rafter Lip/Claw Angle on DP Side, Lower Claw Angle

H18 = SS or S

Hip Rafter Housing Angles

H19 = Hip Rafter Housing Angle on Hip Rafter Rotated into the Roof Surface

H20 = Hip Rafter Housing Angle on DP side of Hip Rafter on top Face

H21 = Hip Rafter Housing Angle on DP side of Hip Rafter on Bottom Face

H22 = Valley Saw Blade Bevel Angle

Valley Sleeper Bevel Angle = 90 - arctan( tan ( SS ) ÷ sin ( P2m ))

Valley Sleeper Bevel Angle = 90 - (C5m + C5a)

------------------------------------------------------------------------------------

Time to make some more test cuts.

Here I cut a 4x4 using
Miter Angle = 90° - 75.38684° = 14.6°
Saw Blade Bevel Angle = 14.03622° = 90° - 14° = 76°.

The test cut post fit next to the Tréteaux Dit Cadet task model post correctly.

I printed out the Parallelogram Prism at a 1" to 1" scale and placed the test post on the paper with the Parallelogram Prism. It fit correctly.

Another view of the post on the Parallelogram Prism.

Saw Blade Bevel Angle set to 76° = 90° - 14°

After testing the Parallelogram Prism post cut I decided to make another sawhorse. However, I didn't have any more 4x4 material. So I used 2x4's. It can be a job site Tréteaux -- Trestle sawhorse.

I cut 4 2x4's with the same miter and saw blade bevel. I layed them out using my Sawhorse template, to make sure they were exactly the same length.

After I cut the legs, I measured 1" from the outside of the leg and used my skillsaw ,set at 0°, to make the plumb cut on the end of the sawhorse leg. When you first cut the sawhorse legs use the same miter and bevel angle at each end of the leg with both cuts going the same direction. If the leg were placed in the correct vertical position in the sawhorse model the top of the saw horses prism cut would represent a level plane. Cutting across the top of the level plane produces the plumb cut on the sawhorse leg.