The 5 Platonic solids:
The Tetrahedron (3 equilateral triangles at each vertex)
The Hexahedron (3 squares at each vertex, cube)
The Octahedron (4 equilateral triangles at each vertex)
The Dodecahedron (3 pentagons at each vertex)
The Icosahedron (5 equilateral triangles at each vertex)
The so-called Platonic Solids are regular polyhedra. “Polyhedra” is a Greek word meaning “many faces.” There are five of these, and they are characterized by the fact that each face is a regular polygon, that is, a straight-sided figure with equal sides and equal angles: All of the edges of the Platonic Solids are Hip Rafters.
Platonic Solid TETRAHEDRON
Platonic Solid TETRAHEDRON
Deck: Equilateral Triangle
Roof Surface Faces: 3 Equilateral Triangles
Deck Angle = 60°
Plan Angle DD = 30.00°
Common Rafter Slope Angle SS = 70.52878°
Hip Rafter Slope Angle R1 = 54.73561°
Dihedral Angle Between Faces = 70.52855°
Hip Rafter Backing Angle = 54.73572°
Platonic Solid Edge Cuts
Hip Rafter Miter Angle = 54.73561°
Hip Rafter Bevel Angle = 45.00°
Hip Rafter Saw Blade Bevel Angle = 30.00°
Stereotomic & Descriptive Geometry for the Tetrahedron (3 equilateral triangles at each vertex)
Hip Rafter Edge Bevel Angles
Platonic Solid Hexahedron (Cube)
Platonic Solid CUBE
Deck: Equilateral Triangle
Roof Surface Faces: 3 x Isosceles Triangle
Deck Angle = 60°
Plan Angle DD = 30.00°
Common Rafter Slope Angle SS = 54.73561°
Hip Rafter Slope Angle R1 = 35.26439°
Dihedral Angle Between Faces = 90°
Hip Rafter Backing Angle = 45°
Platonic Solid Edges
Hip Rafter Miter Angle = 35.26439°
Hip Rafter Bevel Angle = 35.26439°
Hip Rafter Saw Blade Bevel Angle = 30.00°
Stereotomic & Descriptive Geometry for the Hexahedron (3 squares at each vertex, cube)
Hip Rafter Edge Bevel Angles
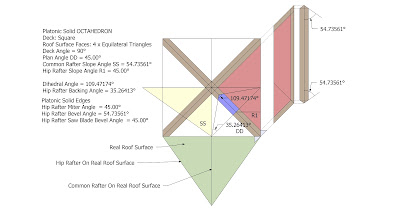
Platonic Solid Octahedron
Platonic Solid OCTAHEDRON
Deck: Square
Roof Surface Faces: 4 x Equilateral Triangles
Deck Angle = 90°
Plan Angle DD = 45.00°
Common Rafter Slope Angle SS = 54.73561°
Hip Rafter Slope Angle R1 = 45.00°
Dihedral Angle = 109.47174°
Hip Rafter Backing Angle = 35.26413°
Platonic Solid Edges
Hip Rafter Miter Angle = 45.00°
Hip Rafter Bevel Angle = 54.73561°
Hip Rafter Saw Blade Bevel Angle = 45.00°
Stereotomic & Descriptive Geometry for the Octahedron (4 equilateral triangles at each vertex)
Hip Rafter Edge Bevel Angles
Platonic Solid Icosahedron
Platonic Solid ICOSAHEDRON
Deck: Pentagon
Roof Surface Faces: 5 x Equilateral Triangles
Deck Angle = 108°
Plan DD = 54.00°
Common Rafter Slope Angle SS = 37.37737°
Hip Rafter Slope Angle R1 = 31.71747°
Dihedral Angle = 138.16038°
Hip Rafter Backing Angle = 20.91981°
Platonic Solid Edges
Hip Rafter Miter Angle = 31.71747°
Hip Rafter Bevel Angle = 58.2825°
Hip Rafter Saw Blade Bevel Angle = 54.00°
Stereotomic & Descriptive Geometry for the Icosahedron (5 equilateral triangles at each vertex)
Hip Rafter Edge Bevel Angles
Platonic Solid Dodecahedron
Platonic Solid DODECAHEDRON
Deck: Equilateral Triangle
Roof Surface Faces: 3 x Isosceles Triangle
Deck Angle = 60°
Plan Angle DD = 30°
Common Rafter Slope Angle SS = 37.37737°
Hip Rafter Slope Angle R1 = 20.90516°
Dihedral Angle = 116.56506°
Hip Rafter Backing Angle = 31.71747°
Platonic Solid Edges
Hip Rafter Miter Angle = 20.90516°
Hip Rafter Bevel Angle = 31.71747°
Hip Rafter Saw Blade Bevel Angle = 30.00°
Stereotomic & Descriptive Geometry for the Dodecahedron (3 pentagons at each vertex)
Hip Rafter Edge Bevel Angles















No comments:
Post a Comment
Note: Only a member of this blog may post a comment.