Roof Framing Geometry: Pentahedron and Non-Rectangular Sections

Pentahedron and Non-Rectangular Sections Study by Joe Bartok

__________________________________________________

warlock_rhombic_nr_solution.pdf

warlock_rhombic_javascript_solution.pdf
__________________________________________________

When I compare the Golden Rhombus and the current Offset Rotated Rafters this Compound Angle Formula works all around:
μ = arctan (sin Angle at Rafter Peak ÷ tan Blade Bevel Angle)

Golden Rhombus (my study half-split the roof angle but the formula works just as well for your equal width Hips solution):
μ = arctan (sin (90° – 27.73230°) ÷ tan (90° – 47.05622°) = 43.56300°
β = 90° – R1 = 90° – 27.73230° = 62.26770°
α = C5 = 16.04506°

70° Offset 12/12 Side Rafter ... Claw Angle Version:
μ = arctan (sin 28.71825° ÷ tan 5.36467°) = 78.94194° (Angle on Upper Shoulder of Offset Rafter)
β = 28.71825° (Upper Claw Angle)
α = 13.99545° (Rotated Rafter Backing Angle)

70° Offset 12/12 Side Rafter ... Plumb Line Version:
μ = arctan (sin (90° – 43.21918°) ÷ tan 16.86990°) = 67.40640° (Angle on Upper Shoulder of Offset Rafter)
β = 90° – R1 = 90° – 43.21918° = 46.78082°
α = 13.99545° (Rotated Rafter Backing Angle)

Looking good, but a long way to go yet.
______________________________________________

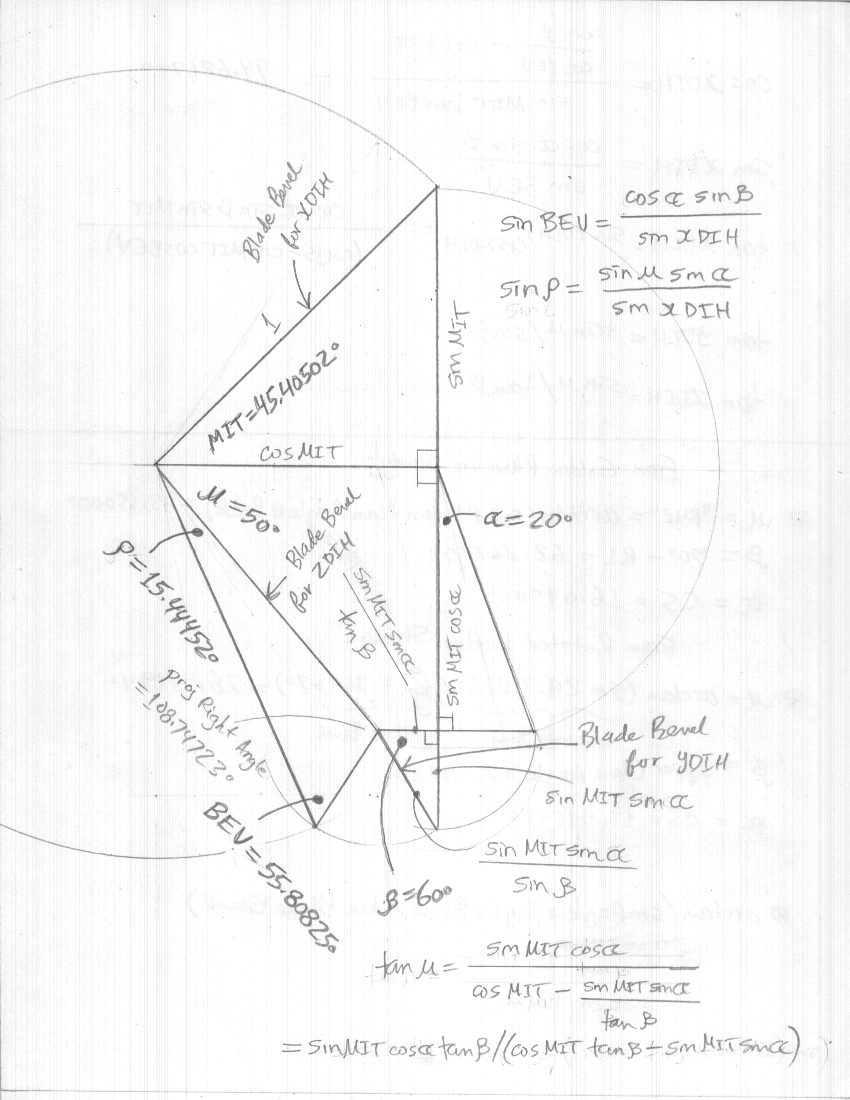
Development of a Pentahedron describing a Non-Rectangular Section, given μ, β and α. After the first few steps the rest of the drawing falls into place.

Setting a different reference length = 1 has produced a few new relationships:

ρ = (90° – BEV) – arctan (cos YDIH ÷ tan β)

Blade Bevel for YDIH = arcsin (tan β ÷ tan (BEV + ρ))

MIT = arctan (sin μ tan β ÷ (cos α cos μ tan β + sin μ sin α))

Test firing the formulas on real Hip roof studies:

Golden Rhombus ... Half-split Roof Angle

μ = arctan (sin (90° – 27.73230°) ÷ tan (90° – 47.05622°) = 43.56300°

β = 90° – R1 = 90° – 27.73230° = 62.26770°

α = C5 = 16.04506°

ρ = Offset Rafter Slope Angle – arctan (tan Main Hip Slope Angle sin Blade Bevel

ρ = 30.79574° – arctan (tan 27.73230° sin (90° – 47.05622°) = 11.08972°

MIT = arctan (sin 43.56300° tan 62.26770° ÷ (cos 16.04506° cos 43.56300° tan 62.26770° + sin 43.56300° sin 16.04506°)) = 40.86615°

70° Offset 12/12 Side Rafter ... Claw Angle Version:

μ = arctan (sin 28.71825° ÷ tan 5.36467°) = 78.94194° (Angle on Upper Shoulder of Offset Rafter)

β = 28.71825° (Upper Claw Angle)

α = 13.99545° (Offset Rafter Backing Angle)

ρ = (90° – Trace Angle on Main Hip) – arctan (tan (90° – Upper Claw Angle) sin Blade Bevel)

ρ = (90° – 55.50766°) – arctan (tan (90° – 28.71825°) sin 5.36467°) = 24.80855°

MIT = arctan (sin 78.94194 tan 28.71825 ÷ (cos 13.99545 cos 78.94194 tan 28.71825 + sin 78.94194 sin 13.99545)) = 57.74662°

70° Offset 12/12 Side Rafter ... Plumb Line Version:

μ = arctan (sin (90° – 43.21918°) ÷ tan 16.86990°) = 67.40640° (Angle on Upper Shoulder of Offset Rafter)

β = 90° – R1 = 90° – 43.21918° = 46.78082°

α = 13.99545° (Offset Rafter Backing Angle)

ρ = Main Hip Slope Angle – arctan (tan Offset Rafter Slope Angle sin Blade Bevel)

ρ = 30.96374° – arctan (tan 43.21918 sin 16.86990°) = 15.71018°

MIT = arctan (sin 67.40640° tan 46.78082 ÷ (cos 13.99545 cos 67.40640° tan 46.78082 + sin 67.40640° sin 13.99545)) = 57.74661°

There doesn’t appear to be a pattern for the formulas for ρ in terms of the roof angles, but:

... 30.79574° and 30.96374° are really 90° – Trace Angles for their respective rafters

... Main Hip Slope Angle and Offset Rafter Slope Angle are 90° – Upper Claw Angle are the complements of the angles at their respective rafter peaks.

ρ = 90° – Trace Angle – arctan( sin Blade Bevel ÷ tan Angle at Rafter Peak)???

Penathedron and Non-Rectangular Section Test

Intersecting Hip Rafters – Warlock Cut, Upper Shoulder Hip B

Angle on Hip B Upper Left Shoulder = 37.65287°

Blade Bevel @ 37.65287° = 55.39851°

μ = arctan (sin 37.65287° ÷ tan 55.39851°) = 22.85244° = Angle on Hip B Upper Right Shoulder ... expected that, the rafter section is rectangular

β = 37.65287° = Angle on Hip B Upper Left Shoulder

α = 0° ... at first glance it might seem like this should be 45°, but there is no backing or rotation angle here

MIT = 37.65287°

BEV = 43.14862° (Trace Angle on Hip A)

ρ = 0°

Projected Right Angle = 136.85138°

Supplementary Angle = 43.14862° (= Trace Angle on Hip A)

Blade Bevel for XDIH = 55.39850°

Blade Bevel for YDIH = 26.71762° (Blade Bevel @ 22.85244°)

Blade Bevel for ZDIH = 55.39850° (= Blade Bevel for XDIH)

The code returned angles for a tetrahedron (which we already know works here). This isn't telling me anything new or lending insight as to an easier means of drawing the intersection.