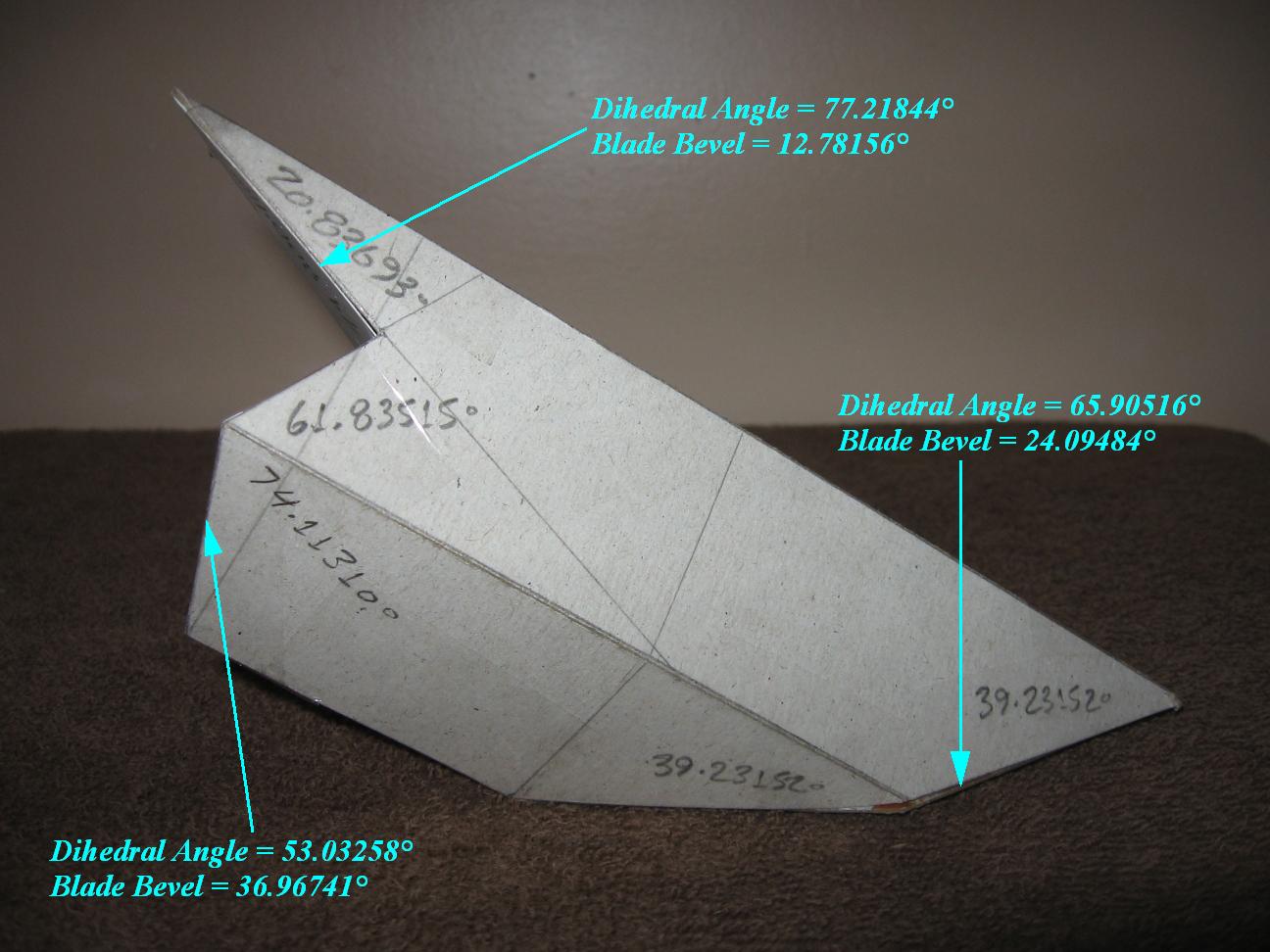
Here's a picture of the studies for the winter of 2014 by Joe Bartok. Joe's studies include the Golden Rhombus, Golden Rhombus Parallelogram, Trèteaux Angles -- Trestle Angles -- trèteau à devers, Devers De Pas -- DP Line, trait carré -- TC, when hips collide, rotated rafters, rotated hip rafters, Warlock Cut, Warlock Rhombic, Non-Rectangular Sections, Pentahedron and Non-Rectangular Sections, Trirectangular Tetrahedron, Raccord--Origami 3D models all with upper and lower claw angles.
There's been a lot of trigonometry in Joe's studies, but there's also been a lot of geometry in his drawings leading up to his cardboard models. It was from his geometry, that he developed on his own, without looking at the French or German books, that some of my Roof Framing Geometry Proposition – Axioms were based on. The German Dachstuhlbau geometrie method or the 'Art du Trait', developed in the 13th century by the French are all based on stereotomtic principles developed 500+ BC for the stone masons. Whether we're using the Basiswissen Dachfläche Ausmittlung or Shiftungen method developed by the German Zimmerman or the Art Du Trait, “Compagnonnage” system in France by the French Compagnons, both methods are for developing the intersection of 3D planes drawn in 2D space just like Joe's geometric drawings.
Quote from Joe
_____________________________________________________________
Other than glimpses on the Internet I’ve never read or studied the books by Louis Mazerolle et al. For sure the timber framers and carpenters of the past (and some today) would have been aware of and understood the reference lines and planes required to lay out their work. But I've wondered if it was it done to an organized, universal set of rules (
http://sbebuilders.blogspot.ca/2014/04/roof-framing-geometry-propositions.html)? Or were they locating the nodes or intersects of lines and connecting the points (like I did for the Warlock Cuts and offset rafters)?
My roof framing geometry horizons have certainly expanded these last two months, lots of new ways to look at the geometry. What's really cool about this is that the seemingly "different" intersections all tie into or are related to one another.
_____________________________________________________________