In Euclidean geometry, a rhombus (◊), plural rhombi or rhombuses, is a simple (non-self-intersecting) quadrilateral whose four sides all have the same length.
A quadrilateral with four sides of equal length.
The two diagonals of a rhombus are perpendicular.
Golden rhombus
In geometry, a golden rhombus is a rhombus whose diagonals are in the ratio 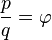 , where
, where  is the golden ratio.
is the golden ratio.
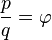 , where
, where  is the golden ratio.
is the golden ratio.
Hip Rafter Diagonal A ÷ Hip Rafter Diagonal B = Golden Ratio = 1.61833
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It has 60 edges and 32 vertices of two types. It is a Catalan solid, and the dual polyhedron of the icosidodecahedron.
The ratio of the long diagonal to the short diagonal of each face is exactly equal to the golden ratio, φ, so that the acute angles on each face measure2 tan−1(1/φ) = tan−1(2), or approximately 63.43°. A rhombus so obtained is called a golden rhombus.
_____________________________________________________________________________________
Hamp Stevens, an mathematical artist asked for help with the hip rafter head cuts on his Parallelogram Roof. The roof is based on the face of the "dual" of an "Icosidodecahedron", which is an "Archimedean Solid". The dual of an Icosidodecahedron is known as a "Rhombic Triacontahedron" and it consists of 30 parallelograms. He's only using one of the parallelograms for the ground plan of hip roof. This parallelogram is an golden rhombus. With the four edges equal in length, the diagonals of the parallelogram are perpendicular and the eave angle, arctan(2) =63.43494° , produces the golden ratio of 1.61803399 for the diagonals of the parallelogram.
Hamp Stevens website with wooden polyhedra
Hamp Stevens website with wooden polyhedra
The ground plan for the golden rhombus parallelogram is easy to layout. Make a triangle with the base leg 1/2 the length of the other leg and it automatically forms a triangle with the 63.43494° eave angle.
The intersection of the two hip rafter runs are perpendicular, so the miter angle for the two hip rafters in plan view are 45°.
Hip Rafter Bevel Angle @ Peak = arctan(cos(R1) ÷ tan(Plan Miter Angle))
Hip Rafter A Bevel Angle @ Peak = arctan(cos(18) ÷ tan(45)) = 43.56300
Hip Rafter B Bevel Angle @ Peak = arctan(cos(27.73233) ÷ tan(45)) = 41.51304
Saw
Blade Bevel Angle @ Peak = arctan(cos(18°) ÷ tan(43.56300°) = 45.00°
Saw Blade Bevel Angle @ Peak = arctan(cos(27.73233°) ÷ tan(41.51304°) = 45.00°
Hip Rafter A
Roof Eave Angle =
63.43490
SS = Main Rafter Slope Angle = 31.71750
S = Adjacent Rafter Slope Angle = 31.71750
DD = Main Plan Angle = 31.71745
D = Adjacent Plan Angle = 31.71745
R1 = Hip Rafter Slope Angle = 18.0000Hip Rafter foot Side Cut Angle = 30.44636°
SS = Main Rafter Slope Angle = 31.71750
S = Adjacent Rafter Slope Angle = 31.71750
DD = Main Plan Angle = 31.71745
D = Adjacent Plan Angle = 31.71745
R1 = Hip Rafter Slope Angle = 18.0000Hip Rafter foot Side Cut Angle = 30.44636°
Hip Rafter foot Saw Blade Bevel Angle = 58.28255°
Hip Rafter peak Side Cut Angle = 43.56300°
Hip Rafter peak Side Cut Angle = 43.56300°
Hip Rafter peak Saw Blade Bevel Angle = 45.00°
Hip Rafter B
Roof Eave Angle = 116.56510
SS = Main Rafter Slope Angle = 31.71750
S = Adjacent Rafter Slope Angle = 31.71750
DD = Main Plan Angle = 58.28255
D = Adjacent Plan Angle = 58.28255
R1 = Hip Rafter Slope Angle = 27.73233
Hip Rafter foot Side Cut Angle = 55.07574°
Hip Rafter B
Roof Eave Angle = 116.56510
SS = Main Rafter Slope Angle = 31.71750
S = Adjacent Rafter Slope Angle = 31.71750
DD = Main Plan Angle = 58.28255
D = Adjacent Plan Angle = 58.28255
R1 = Hip Rafter Slope Angle = 27.73233
Hip Rafter foot Side Cut Angle = 55.07574°
Hip Rafter foot Saw Blade Bevel Angle = 31.71745°
Hip Rafter peak Side Cut Angle = 41.51304°
Hip Rafter peak Saw Blade Bevel Angle = 45.00°
Hip Rafter peak Side Cut Angle = 41.51304°
Hip Rafter peak Saw Blade Bevel Angle = 45.00°
Saw Blade Bevel Angle @ Foot = arctan(cos(18°) ÷ tan(30.44636°) = 58.28255°
Saw Blade Bevel Angle @ Peak = arctan(cos(27.73233°) ÷ tan(55.07574°) = 31.71745°
My 4x4 scrap test model. It's harder screwing the hip rafters together correctly than cutting them. This model isn't perfect, but the 45° saw blade bevel angle works. It's a typical polyhedron. If the cuts aren't 100% correct, them it will show in the assemblage of the edge pieces.
_________________________________________________________
The 5 Platonic solids:
The Tetrahedron (3 equilateral triangles at each vertex)
The Hexahedron (3 squares at each vertex, cube)
The Octahedron (4 equilateral triangles at each vertex)
The Dodecahedron (3 pentagons at each vertex)
The Icosahedron (5 equilateral triangles at each vertex)
My 4x4 scrap test model. It's harder screwing the hip rafters together correctly than cutting them. This model isn't perfect, but the 45° saw blade bevel angle works. It's a typical polyhedron. If the cuts aren't 100% correct, them it will show in the assemblage of the edge pieces.
_________________________________________________________
Compound Saw Miter and Saw Blade Bevel Angles For Platonic Solids Calculator
The Tetrahedron (3 equilateral triangles at each vertex)
The Hexahedron (3 squares at each vertex, cube)
The Octahedron (4 equilateral triangles at each vertex)
The Dodecahedron (3 pentagons at each vertex)
The Icosahedron (5 equilateral triangles at each vertex)
Archimedean Solids with Jack Rafter Side Cut Angles & Hip Rafter Backing Angles & Dihedral Angles
For Compound Miter Saw Settings (Dihedral Angle + Hip Rafter Backing Angle + Hip Rafter Backing Angle= 180°) Enter Jack Rafter Side Cut Angle and Hip Rafter Backing Angle at this URL below for compound Miter Saw Settings for compound joinery of Archimedean Solids.
For Compound Miter Saw Settings (Dihedral Angle + Hip Rafter Backing Angle + Hip Rafter Backing Angle= 180°) Enter Jack Rafter Side Cut Angle and Hip Rafter Backing Angle at this URL below for compound Miter Saw Settings for compound joinery of Archimedean Solids.
My RafterTools app for android also has the Platonic Solids calculator as well as the Archimedean Solids calculator for compound miter saw settings to cut the edge pieces of the polyhedron laying flat or on edge.









No comments:
Post a Comment
Note: Only a member of this blog may post a comment.